The History of Deep Learning
The history of artificial intelligence is marked by two alternating waves: one of hype and one of pessimism. A wave charecterized by high hopes with great funding, commonly known as AI spring , is usually followed by disillusionment due to unmet promises and the drying up of funding, also known as AI winter.
In this section we will attempt to cover those waves. In all likelihood we will fail at covering all the aspects that lead to the development of modern deep learning, so consider this chapter merely a starting point.
First Wave: Birth of Artificial Neural Networks
McCulloch-Pitts Neuron
Artificial neurons are not exact copies of biological neurons, but we could say that some components were borrowed during the development of artificial neural networks. Our explanations of biological neurons do not fully represent the messy reality, but they are good enough to get us started.
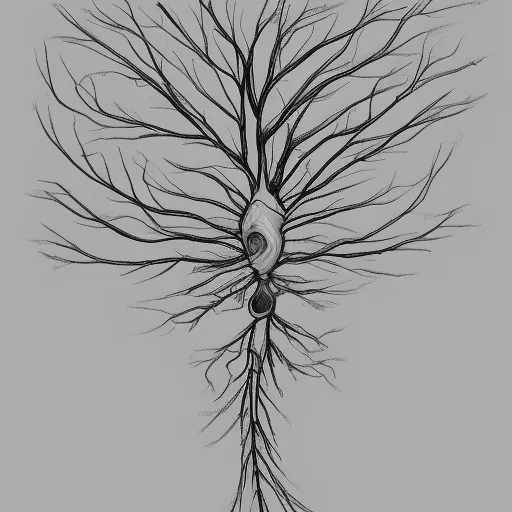
A biological neuron receives inputs through branch-like structures called dendrites which are usually connected to other neurons. The strenghts of signals varies based on the strength of the connections between the neurons. The stronger the connection, the stronger the signal. In the second step the incoming signals are aggregated in the center (the nucleus) of the neuron. If the cumulative strength of all inputs is larger than some threshold, the signal travels over the axon (the long tail of the neuron) to the connected neurons. In that case we also say that the neuron is active.
Warren McCulloch and Walter Pitts [1] tried to come up with a mathematical model of the brain that would be able to simulate a biological neuron and thus developed the first artificial neuron. Let us assume for a second that we are in the position of McCulloch and Pitts and would like to emulate the above described behaviour. What would be the key ingredients of an artificial neuron?
For once the neuron needs to to receive inputs and to adjust their strength. As we are dealing with a mathematical model, the inputs must be numerical. In the examples below we will assume that all the inputs amount to 1 in order to make the illustrations more intuitive, but generally speaking the inputs can assume any numerical form. The strength of the signal can be changed with the help of a scaling factor, called weight. We can adjust the strength of the input by multiplying the input x undefined with a corresponding weight w undefined . If the weight is above 1, the input signal is amplified, if the weight is between 0 and 1 the input signal is dampened. The strength of the signal can also be reversed by multiplying the signal with a negative weight.
Info
Inside the artificial neuron the strength of the input signal x undefined is adjusted with the help of the weight w undefined by multiplying the input by the weight: x*w undefined .
Below is a simple interactive example that allows you to vary the weight and to observe how the strength of the signal changes. The color of the signal is blue when the scaled signal is positive and red when it becomes negative. The stroke width of the signal depends on the size of the weight.
| Variable | Value |
|---|---|
| Input x undefined | 1 |
| Weight w undefined | 1 |
| Scaled Value x * w undefined | 1 |
In the next step we need to figure out the behaviour of the neuron when we deal with multiple inputs. Similar to the biological neuron the input signals need to be scaled individually and accumulated. In the mathematical model of McCulloch and Pitts the weighted inputs are simply added together.
Multiplying each input x_j undefined by a corresponding weight w_j undefined and calculating the sum out of the products is called a weighted sum. Mathematically we can express this idea as \sum_j x_jw_j undefined , where j undefined is the index of the input and the corresponding scaling factor.
In the interactive example below, you can vary the weights of two inputs and observe how the weighted signals are accumulated.
| Variable | Value |
|---|---|
| Input x_1 undefined | 1 |
| Weight w_1 undefined | 1 |
| Scaled Value x_1 * w_1 undefined | 1 |
| Input x_2 undefined | 1 |
| Weight w_2 undefined | 1 |
| Scaled Value x_2 * w_2 undefined | 1 |
| Weighted Sum \sum_j x_j w_j undefined | 2.00 |
The final component that our artificial neuron needs, is the ability to become active based on the accumulated input strength.
Info
A function that takes the weighted sum as input and determines the activation status of a neuron is commonly refered to as the activation function.
McCulloch and Pitts used a simple step function as the activation function. If the weighted sum of the inputs is above a threshold \theta undefined the output is 1, else the output is 0.
f(\mathbf{w}) = \left\{ \begin{array}{rcl} 0 & for & \sum_j x_j w_j \leq \theta \\ 1 & for & \sum_j x_j w_j > \theta \\ \end{array} \right. undefinedBelow is an interactive example of a step function with a \theta undefined of 0. You can move the slider to observe how the shape of the step function changes due to a different \theta undefined .
The last interactive example allows you to vary two weights w_1 undefined , w_2 undefined and the threshold \theta undefined . Observe how the flow of data changes based on the weights and the threshold.
| Variable | Value |
|---|---|
| Input x_1 undefined | 1 |
| Weight w_1 undefined | 1 |
| Scaled Value x_1 * w_1 undefined | 1 |
| Input x_2 undefined | 1 |
| Weight w_2 undefined | 1 |
| Scaled Value x_2 * w_2 undefined | 1 |
| Weighted Sum \sum_j x_j w_j undefined | 2.00 |
| Theta \theta undefined | 0.00 |
| Output | 1.00 |
In practice we replace the threshold \theta undefined by a so called bias b undefined . To illustrate the procedure let us assume that the weighted sum corresponds to the threshold.
\sum_j x_j w_j = \theta undefinedWe can bring \theta undefined to the other side of the equation.
\sum_j x_j w_j - \theta = 0 undefinedAnd define the negative threshold \theta undefined as the bias b undefined .
b = -\theta \\ \sum_j x_j w_j + b = 0 \\ undefinedWhich leads to the following equation for the threshold function.
f(\mathbf{w}, b) = \left\{ \begin{array}{rcl} 0 & for & \sum_j x_j w_j + b \leq 0 \\ 1 & for & \sum_j x_j w_j + b > 0 \\ \end{array} \right. undefinedIt might seem like all we do is reformulate the equation, but the idea is actually really powerful. We do not assume to know the bias b undefined . Just as the weights w_j undefined in the equation, the bias is a learnable parameter. When we talk about \theta undefined on the other hand we assume to know the threshold.
What we discussed so far is a fully fledged artificial neuron. The representation of the strength of the signal through a weight w undefined , the accumulation of the input signals through summation and the ability to declare the neuron as active or inactive through an activation function is still at the core of modern deep learning. The ideas developed by McCulloch and Pitts stood the test of time.
Perceptron
McCulloch and Pitts provided an architecture for an artificial neuron that is still used today. Yet they did not provide a way for a neuron to learn.
Info
Learning in machine learning means changing weights w undefined and the bias b undefined , such that the neuron gets better and better at a particular task.
The perceptron developed by Frank Rosenblatt[2] builds upon the idea of McCulloch and Pitts and adds a learning rule, that allows us to use an artificial neuron in classification tasks.
Imagine we have a labeled dataset with two features and two possible classes, as indicated by the colors in the scatterplot below.
It is a relatively easy task for a human being to separate the colored circles into the two categories. All we have to do is to draw a line that perfectly separates the two groups.
The perceptron algorithm is designed to find such a line in an automated way. In machine learning lingo we also call such a line a decision boundary.
"Perceptrons"
The McCulloch and Pitts neuron can be used to simulate logical gates, that are commonly used in comuter architectures and researchers assumed at the time that these logical gates can be used as buidling blocks to simulate a human brain.
The or gate for example produces an output of 1 if either input 1 or input 2 amount to 1.
| Input 1 | Input 2 | Output |
|---|---|---|
| 0 | 0 | 0 |
| 0 | 1 | 1 |
| 1 | 0 | 1 |
| 1 | 1 | 1 |
We can use the perceptron algorithm to draw a decision boundary between the two classes.
The and gate on the other hand produces an output of 1 when input 1 and input 2 amount to 1 respectively.
| Input 1 | Input 2 | Output |
|---|---|---|
| 0 | 0 | 0 |
| 0 | 1 | 0 |
| 1 | 0 | 0 |
| 1 | 1 | 1 |
The decision boundary is easily implemented.
Marvin Minsky and Seymour Papert published a book named "Perceptrons" [3] in the year 1969. In that book they showed that a single perceptron is not able to simulate a so called xor gate. The xor gate (exclusive or) outputs 1 only when one and only one of the inputs is 1.
| Input 1 | Input 2 | Output |
|---|---|---|
| 0 | 0 | 0 |
| 0 | 1 | 1 |
| 1 | 0 | 1 |
| 1 | 1 | 0 |
If you try to separate the data by drawing a single line, you will come to the conclusion, that it is impossible.
Yet you can separate the data by using a hidden layer. Essentially you combine the output from the or gate with the output from the and gate and use those outputs as inputs in the neuron of the next layer.
| Input 1 | Input 2 | OR Output | AND Output | XOR |
|---|---|---|---|---|
| 0 | 0 | 0 | 0 | 0 |
| 0 | 1 | 1 | 0 | 1 |
| 1 | 0 | 1 | 0 | 1 |
| 1 | 1 | 1 | 1 | 0 |
That makes the data separable with a single line.
First AI Winter
It is not easy to pin down the exact date of the beginning and the end of the first AI winter. Often the book by Minsky and Papert is considered to have initiated the decline of research in the field of artificial neural networks, even thogh it was known at the time, that multilayer perceptrons are able to solve the xor problem. More likely the general disillusionment with AI systems and the overpromies that were made by the research community lead to drastically reduced funding. Roughly speaking the winter held from the beginning of 1970's to the beginning fo 1980's.
Second Wave: Neural Networks in the Golden Age of Expert Systems
The second wave of artificial intelligence research, that started in the early 1980's, was more favourable towards symbolic artificial intelligence. Symbolic AI lead to so called expert systems, where experts infuse their domain knowledge into the program in the hope of being able to solve intelligence though logic and symbols.
Nevertheless there were some brave souls who despite all the criticism of neural networks were able to endure and innovate. The groundbreaking research that was done in the second wave of artificial intelligence enabled the success and recognition that would only come in the third wave of AI.
Backpropagation
The perceptron learning algorithm only works for relatively easy problems. For a very long time it was not clear how we could train neural networks when we are faced with a complex problem (like image classification) and the network has hidden layers. In 1986 Rumelhart, Hinton and Williams published a paper that described the backpropagation algorithm [4] . The procedure combined gradient descent, the chain rule and efficient computation to form what has become the backbone of modern deep learning. The algorithm is said to have been developed many times before 1986, yet the 1986 paper has popularized the procedure.
The backpropagation algorithm will be covered in a dedicated section, but let us shortly cover the meaning of the name "backpropagation". This should give you some intuition regarding the workings of the algorithm. Essentially modern deep learning consists of two steps: feedforward and backpropagation.
So far we have only considered the feedforward step. During this step each neuron processes its corresponding inputs and its outputs are fed into the next layer. Data flows forward from layer to layer until final outputs, the predictions of the model are generated.
Once the neural network has produced outputs, they can be compared to the actual targets. For example you can compare the predicted house price with the actual house price in your training dataset. This allows the neural network to compute the error between the prediction and the so called ground truth. This error is in turn propagated backwards layer after layer and each weight (and bias) is adjusted proportionally to the contribution of that the weight to the overall error.
The invention of the backpropagation algorithm was the crucial discovery that gave us the means to train neural networks with billions of parameters.
Recurrent Neural Networks
The second wave additionally provided us with a lot of research into the field of recurrent neural networks like the Hopfield network[5] and LSTM[6] .
Unlike feedforward neural networks, a recurrent neural network (RNN) has self reference. When we deal with sequential data like text or stock prices, the output that is produced from the previous time step in the sequence (e.g. first word of the sentence) is used as an additional input for the next time step of the sequence (e.g. second word in the sentence).
Convolutional Neural Networks
The area of computer vision also made great leaps during the second wave. The most prominent architecture that was developed during that time are the convolutional neural networks (CNN). The development of CNNs a has a rich history, that started with research into the visual cortex of cats [7] , which lead to the development of the first convolutional architecture by Kunihiko Fukushima, neocognitron[8] , which in turn lead to the incorporation of backpropagation into the CNN architecture by Yann LeCun[9] .
In a convolutional neural network we have a sliding window of neurons, that focuses on one area of a picure at a time. Unlike fully connected neural networks, this architecture takes into account, that nearby pixels in 2d space are related. Even today convolutional neural networks produce state of the art results in computer vision.
NeurIPS
Last but not least, in the year 1986 the conference and workshop on neural information processing systems (NeurIPS) was proposed. NeurIPS is a yearly machine learning conference that is still held to this day.
Second AI Winter
The expert systems failed to deliver the promised results, which lead to the second AI winter. The winter started in the mid 1990's and ended in the year 2012.
Third Wave: Modern Deep Learning
In hindsight we can say that deep neural networks required at least three components to become successful: algorithmic improvements, large amounts of data and computational power.
Algorithms: ReLU
Many algorithmic advances were made that allowed researchers to improve the performance of neural networks, therefore we can only scratch the surface in this chapter. The one that seems trivial on the surface, but is actually one of the most significant innovations in deep leaning was the introduction of the rectified linar unit (ReLU) as an activation function[10] [11] .
This activation function returns 0 when \sum_j x_j w_j +b \leq{0} undefined and \sum_j x_j w_j + b undefined otherwise. In other words, the activation function retains positive signals, while the function does not become active for negative signals.
Why this type of function is advantageous will be discussed in a dedicated section. For know it is sufficient to know, that the backpropagation algorithm works extremely well with the ReLU activation function.
Data: ImageNet
While most researchers focused only on the algorithmic side of deep learning, in the year 2006 Fei-Fei Li began working on collecting images for a dataset suitable for large scale vision tasks. That dataset is known as ImageNet[12] .
Nowadays we realize what immense role data plays in deep learning and how data hungry deep learning algorithms are [1] .
The performance of classical machine learning algorithms improves when we increase the amount of data for training, but after a while the rate of improvement is almost flat.
Deep learning algorithms on the other hand have a much steeper curve. The more data you provide, the better the overall performance of the algorithm. Deep learning scales extremely well with the amount of data.
When ImageNet became publicly available to researchers, the potential to scale an artificial neural network to achieve unprecedented performance came into fruition.
But therein also lies a weakness of deep learning. Unless you have at least several tens of thousands of samples for training, neural networks will not shine and you should use some traditional algorithm like decision trees or support vector machines. Compared to humans that can utilize their common sense to learn new concepts fairly quickly, neural networks can be extremely inefficent.
Computation: GPU
Graphics processing units (GPU) were developed independently of deep learning for the use in computer games. In a way it was a happy accident that the same technology that powers the gaming industry is compatible with deep learning. Compared to a CPU, a graphics card posesses thousands of cores, which enables extreme parallel computations. Graphics cards suddenly allowed researchers to train a model that would take months or even years in a matter of mere days.
AlexNet
As part of the 2012 ImageNet competition Alex Krizhevsky, Ilya Sutskever and Geoffrey Hinton created a convolutional neural network called AlexNet[13] . The neural network beat the competition by a large margin combining state of the art deep learning techniques, Nvidia graphics cards for computation and the large scale ImageNet dataset. This moment, often called the ImageNet moment, is regarded as the birthday of modern day deep learning.
Aftershock
The impact that AlexNet had on the artificial intelligence community and the general population is hard to quantify, but just a decade after the release things have changed dramatiacally. It became quickly apparent that AlexNet is just the beginning. The amount of research has skyrocketed and provided new state of the art results for ImageNet, until the competition was declared as solved. New online courses, books, blog post and YouTube videos were published on a regular basis, which in turn allowed beginners to get immersed in this fascinating topic. AI research companies like DeepMind and OpenAI were founded and existing tech companies like Google and FaceBook created their own research laboratories. Deep learning frameworks like TensorFlow and PyTorch were opensourced, which reduced the cost and time needed to conduct research and deploy industry grade models.
While it does not look like we are running out of steam yet with our innovations in deep learning, many researchers seem to agree that deep learning is not our last invention in artificial intelligence. Yet there also seems to be a consensus, that no matter how artificial intelligence of the future will look like, deep learning will play a major role in our develompent of a much more general intelligence. This is a great time to learn about deep learning.