Train, Test, Validate

Intuitively we understand that overfitting leads to a model that does not generalize well to new unforseen data, but we would also like to have some tools that would allow us to measure the level of overfitting during the training process. It turns out that splitting the dataset into different buckets, called sets is essential to achieve the goal of measuring overfitting.

Data Splitting

All examples that we covered so far assumed that we have a training dataset. In practice we split the dataset into preferably 3 sets. The training set, the validation set and the test set.

The training set contians the vast majority of available data. It is the part of the data that is actually used to train a neural network. The other sets are never used to directly adjust the weights and biases of a neural network.

The validation set is also used in the training process, but only during the performance measurement step. The validation set allows us to simulate a situation, where the neural network encounters new data. After each epoch (or batch) we use the training and the validation sets separately to measure the loss. At first both losses will decline, but after a while the validation loss might start to increase again, while the training loss keeps decreasing. This is a strong indication that our model overfits to the training data. The larger the divergence, the larger the level of overfitting.

When we encounter overfitting we will most likely change several hyperparameters of the neural network and apply some techniques in order to reduce overfitting. It is not unlikely that we will continue doing that until we are satisfied with the performance. While we are not using the validation dataset directly in training, we are still observing the performance of the validation data and adjust accordingly, thus injecting our knowledge about the validation dataset into the training of the weights and biases. At some point it becomes hard to argue that the validation dataset represents completely unforseen data. The test set on the other hand is neither touched nor seen during the training process at all. The intention of having this additional dataset is to provide a method to test the performance of our model when it encounters truly never before seen data. We only use the data once. If we find out that we overfitted to the training and the validation dataset, we can not go back to tweak the parameters, because we would require a completely new test dataset, which we might not posess.

While there are no hard rules when it comes to the proportions of your splits, there are some rules of thumb. A 10-10-80 split is for example relatively common.

In that case we want to keep the biggest chunk of our data for training and keep roughly 10 percent for validation and 10 percent for testing.

We have a couple of options, when we split the dataset. The simplest approach would be to separate the data randomly. While this type of split is easy to implement, it might pose some problems. In the example below we are faced with a dataset consisting of 10 classes (numbers 0 to 9) with 10 samples each. In the random procedure that we use below we generate a random number between 0 and 1. If the number is below 0.5 we assign the number to the blue split, otherwise the number is assigned to the red split.

If you observe the splits, you will most likely notice that some splits have more numbers of a certain category. That means that the proportions of some categories in the two splits are different. This is especially a problem, when some of the categories have a limited number of samples. We could end up creating a split that doesn't include a particular category at all.

A stratified split on the other hand tries to keep the proportions of the different classes consistent.

Now let's see how we can create and utilize the three datasets in PyTorch and whether theory matches the practice.

import torch 
import torch.nn as nn
import torch.optim as optim
from torch.utils.data import DataLoader, Subset
from torchvision.datasets import MNIST
from torchvision import transforms as T
from sklearn.model_selection import train_test_split

import matplotlib.pyplot as plt

The MNIST object does not provide any functionality to get a validation dataset out of the box. We will download the training and testing datasets first and divide the training dataset into two parts: one for training one for validation.

train_validation_dataset = MNIST(root="../datasets/", train=True, download=True, transform=T.ToTensor())
test_dataset = MNIST(root="../datasets", train=False, download=False, transform=T.ToTensor())

We use the train_test_split function from sklearn to generate indices. Those indices indicate if a particular sample is going to be used for training or testing. We conduct a stratified split to keep the distribution of labels consistent. 90% of the data is going to be used for training and 10% for validation.

stratify = train_validation_dataset.targets.numpy()
train_idxs, val_idxs = train_test_split(
                                range(len(train_validation_dataset)),
                                stratify=stratify,
                                test_size=0.1)

To separate the dataset we use the Subset class which takes the original dataset and the indices and returns the modified dataset, where the samples that are not contained in the index list have been filtered out.

train_dataset = Subset(train_validation_dataset, train_idxs)
val_dataset = Subset(train_validation_dataset, val_idxs)

We keep the parameters similar to those in the previous section, but increase the number of epochs to show the effect of overfitting.

# parameters
DEVICE = ("cuda:0" if torch.cuda.is_available() else "cpu")
NUM_EPOCHS=50
BATCH_SIZE=32
HIDDEN_SIZE_1 = 100
HIDDEN_SIZE_2 = 50
NUM_LABELS = 10
NUM_FEATURES = 28*28
ALPHA = 0.1

Now we have everything that we require to create the three dataloaders: one for training, one for validating, one for testing.

train_dataloader = DataLoader(dataset=train_dataset, 
                              batch_size=BATCH_SIZE,
                              shuffle=True,
                              drop_last=True,
                              num_workers=4)

val_dataloader = DataLoader(dataset=val_dataset, 
                              batch_size=BATCH_SIZE,
                              shuffle=False,
                              drop_last=False,
                              num_workers=4)

test_dataloader = DataLoader(dataset=test_dataset, 
                              batch_size=BATCH_SIZE,
                              shuffle=False,
                              drop_last=False,
                              num_workers=4)

We create the track_performance() function to calculate the average loss and the accuracy of the model.

def track_performance(dataloader, model, criterion):
    # switch to evaluation mode
    num_samples = 0
    num_correct = 0
    loss_sum = 0
    
    # no need to calculate gradients
    with torch.inference_mode():
        for batch_idx, (features, labels) in enumerate(dataloader):
            features = features.view(-1, NUM_FEATURES).to(DEVICE)
            labels = labels.to(DEVICE)
            logits = model(features)
            
            predictions = logits.max(dim=1)[1]
            num_correct += (predictions == labels).sum().item()
            
            loss = criterion(logits, labels)
            loss_sum += loss.cpu().item()
            num_samples += len(features)
    
    # we return the average loss and the accuracy
    return loss_sum/num_samples, num_correct/num_samples

The train_epoch() function trains the model for a single epoch.

def train_epoch(dataloader, model, criterion, optimizer):
    for batch_idx, (features, labels) in enumerate(train_dataloader):
        # move features and labels to GPU
        features = features.to(DEVICE)
        labels = labels.to(DEVICE)

        # ------ FORWARD PASS --------
        output = model(features)

        # ------CALCULATE LOSS --------
        loss = criterion(output, labels)

        # ------BACKPROPAGATION --------
        loss.backward()

        # ------GRADIENT DESCENT --------
        optimizer.step()

        # ------CLEAR GRADIENTS --------
        optimizer.zero_grad()

The train() function simply loops over the number of epochs and puts measures the performance after each iteration. The results are saved in the history dictionary.

def train(epochs, train_dataloader, val_dataloader, model, criterion, optimizer):
    # track progress over time
    history = {"train_loss": [], "val_loss": [], "train_acc": [], "val_acc": []}

    for epoch in range(epochs):
        train_epoch(train_dataloader, model, criterion, optimizer)
        
        # ------TRACK LOSS and ACCURACY --------
        train_loss, train_acc = track_performance(train_dataloader, model, criterion)
        val_loss, val_acc = track_performance(val_dataloader, model, criterion)

        history["train_loss"].append(train_loss)
        history["val_loss"].append(val_loss)
        history["train_acc"].append(train_acc)
        history["val_acc"].append(val_acc)

        if (epoch + 1) % 10 == 0 or epoch == 0:
            print(f'Epoch: {epoch+1}/{epochs}|' 
                  f'Train Loss: {train_loss:.4f} |' 
                  f'Val Loss: {val_loss:.4f} |' 
                  f'Train Acc: {train_acc:.4f} |' 
                  f'Val Acc: {val_acc:.4f}')
    return history

The model is identical to the one we have used over the last sections.

class Model(nn.Module):
    def __init__(self):
        super().__init__()
        self.layers = nn.Sequential(
                nn.Flatten(),
                nn.Linear(NUM_FEATURES, HIDDEN_SIZE_1),
                nn.Sigmoid(),
                nn.Linear(HIDDEN_SIZE_1, HIDDEN_SIZE_2),
                nn.Sigmoid(),
                nn.Linear(HIDDEN_SIZE_2, NUM_LABELS),
            )
    
    def forward(self, features):
        return self.layers(features)

model = Model().to(DEVICE)
criterion = nn.CrossEntropyLoss(reduction="sum")
optimizer = optim.SGD(model.parameters(), lr=ALPHA)

We print our metrics for the training and the valdiation dataset. You can see that the model starts to overfit relatively fast.

history = train(NUM_EPOCHS, train_dataloader, val_dataloader, model, criterion, optimizer)

Epoch: 1/50|Train Loss: 0.1983 |Val Loss: 0.2199 |Train Acc: 0.9451 |Val Acc: 0.9372
Epoch: 10/50|Train Loss: 0.0416 |Val Loss: 0.1211 |Train Acc: 0.9871 |Val Acc: 0.9677
Epoch: 20/50|Train Loss: 0.0162 |Val Loss: 0.1297 |Train Acc: 0.9951 |Val Acc: 0.9713
Epoch: 30/50|Train Loss: 0.0141 |Val Loss: 0.1429 |Train Acc: 0.9953 |Val Acc: 0.9727
Epoch: 40/50|Train Loss: 0.0005 |Val Loss: 0.1363 |Train Acc: 1.0000 |Val Acc: 0.9780
Epoch: 50/50|Train Loss: 0.0003 |Val Loss: 0.1428 |Train Acc: 1.0000 |Val Acc: 0.9787

To reinforce our results, we draw the progression for the two datasets.

def plot_history(history):
    fig = plt.figure(figsize=(12, 5))

    fig.add_subplot(1, 2, 1)
    plt.plot(history["train_loss"], label="Training Loss")
    plt.plot(history["val_loss"], label="Validation Loss")
    plt.xlabel("Epochs")
    plt.ylabel("Cross-Entropy")
    plt.legend()
    
    fig.add_subplot(1, 2, 2)
    plt.plot(history["train_acc"], label="Training Accuracy")
    plt.plot(history["val_acc"], label="Validation Accuracy")
    plt.xlabel("Epochs")
    plt.ylabel("Accuracy")
    plt.legend()
    plt.savefig('overfitting.png')
    plt.show()

The divergence due to overfitting is obvious.

plot_history(history)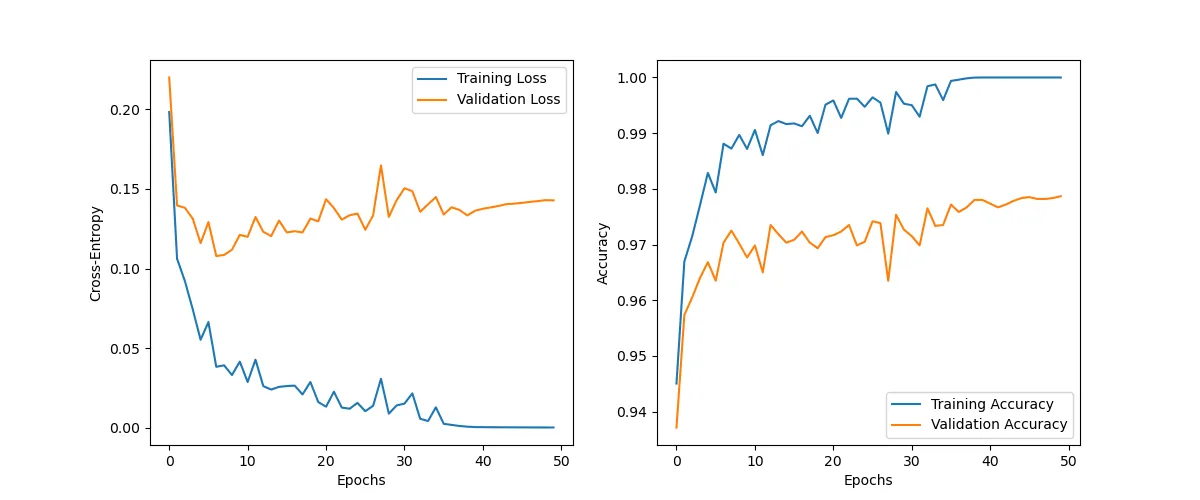

The metrics for the test dataset are relatively close to those based on the validation dataset.

test_loss, test_acc = track_performance(test_dataloader, model, criterion)
print(f'Test Loss: {test_loss:.4f} | Test Acc: {test_acc:.4f}')

Test Loss: 0.1349 | Test Acc: 0.9768

K-Fold Cross-Validation

In the approach above we divided the dataset into three distinct buckets and kept them constant during the whole training process, but ideally we would like to somehow use all available data in training and testing simultaneously. This is especially important if our dataset is relatively small. While we need to keep the test data separate, untouched by training, we can use the rest of the data simultaneously for training and validation by using k-fold cross-validation.

We divide the data (excluding the test set) into k equal sets, called folds. k is a hyperparameter, but usually we construct 5 or 10 folds. Each fold is basically a bucket of data that can be used either for trainig or validation. We use one of the folds for validation and the rest (k-1 folds) for training and we repeat the trainig process k times, switching the fold that is used for validation each time. After the k iterations we are left with k models and k measures of overfitting.

K-Fold cross-validation provides a much more robust measure of performance. At the end of the trainig process we average over the results of the k-folds to get a more accurate estimate of how our model performs. Once we are satisfied with the choise of our hyperparameters, we could retrain the model on the full k folds.

There is obviously also a downside to using k models. Training a neural network just once requires a lot of computaional resources. By using k folds we will more or less increase the training time by a factor of k-1.

To implement k-fold cross-validation with PyTorch we will mostly reuse the code from above, but we still require a couple more components. PyTorch does not offer k-fold out of the box, but once again sklearn is the perfect companion for that purpose. Additionally we import the SubsetRandomSampler. A sampler can be used as an input into the DataLoader object, in order to determine how the samples in a dataset are going to be drawn. A random subset sampler specifically allows us to determine a subset, like a fold and the data is going to be sampled in a random fashion. We could have used the Subset object from above to accomplish the same, but we wanted to teach you different approaches.

from sklearn.model_selection import KFold
from torch.utils.data import SubsetRandomSampler

We use the seed variable as input into KFold and torch.maual_seed. A seed is variable that is used as input into the random number generator. The initial weights and biases of a neural network are generated randomly. By providing a seed into the function torch.manual_seed() we make the parameters of the neural network identical for each of the folds and make our results reproduceble.

epochs = 5
seed = 42
kf = KFold(n_splits=5, shuffle=True, random_state=seed)
for i, (train_index, val_index) in enumerate(kf.split(train_validation_dataset)):
    
    train_subsetsampler = SubsetRandomSampler(train_index)
    val_subsetsampler = SubsetRandomSampler(val_index)
    
    train_dataloader = DataLoader(train_validation_dataset, 
                                  batch_size=BATCH_SIZE, 
                                  sampler=train_subsetsampler)
    val_dataloader = DataLoader(train_validation_dataset, 
                              batch_size=BATCH_SIZE, 
                              sampler=val_subsetsampler)
    torch.manual_seed(seed)
    model = Model().to(DEVICE)
    criterion = nn.CrossEntropyLoss(reduction="sum")
    optimizer = optim.SGD(model.parameters(), lr=ALPHA)
    
    print('-'*50)
    print(f'Fold {i+1}')
    for epoch in range(epochs):
        train_epoch(train_dataloader, model, criterion, optimizer)
        val_loss, val_acc = track_performance(val_dataloader, model, criterion)
        print(f'Epoch: {epoch+1}/{epochs} | Val Loss: {val_loss:.4f} | Val Acc: {val_acc:.4f}')

--------------------------------------------------
Fold 1
Epoch: 1/5 | Val Loss: 0.2120 | Val Acc: 0.9386
Epoch: 2/5 | Val Loss: 0.1681 | Val Acc: 0.9497
Epoch: 3/5 | Val Loss: 0.1360 | Val Acc: 0.9594
Epoch: 4/5 | Val Loss: 0.1169 | Val Acc: 0.9673
Epoch: 5/5 | Val Loss: 0.1295 | Val Acc: 0.9630
--------------------------------------------------
Fold 2
Epoch: 1/5 | Val Loss: 0.1770 | Val Acc: 0.9465
Epoch: 2/5 | Val Loss: 0.1451 | Val Acc: 0.9577
Epoch: 3/5 | Val Loss: 0.1387 | Val Acc: 0.9578
Epoch: 4/5 | Val Loss: 0.1375 | Val Acc: 0.9598
Epoch: 5/5 | Val Loss: 0.1140 | Val Acc: 0.9676
--------------------------------------------------
Fold 3
Epoch: 1/5 | Val Loss: 0.2109 | Val Acc: 0.9397
Epoch: 2/5 | Val Loss: 0.2501 | Val Acc: 0.9206
Epoch: 3/5 | Val Loss: 0.1246 | Val Acc: 0.9616
Epoch: 4/5 | Val Loss: 0.1163 | Val Acc: 0.9650
Epoch: 5/5 | Val Loss: 0.1192 | Val Acc: 0.9650
--------------------------------------------------
Fold 4
Epoch: 1/5 | Val Loss: 0.2243 | Val Acc: 0.9316
Epoch: 2/5 | Val Loss: 0.1793 | Val Acc: 0.9463
Epoch: 3/5 | Val Loss: 0.1270 | Val Acc: 0.9630
Epoch: 4/5 | Val Loss: 0.1172 | Val Acc: 0.9660
Epoch: 5/5 | Val Loss: 0.1158 | Val Acc: 0.9666
--------------------------------------------------
Fold 5
Epoch: 1/5 | Val Loss: 0.1983 | Val Acc: 0.9386
Epoch: 2/5 | Val Loss: 0.1628 | Val Acc: 0.9517
Epoch: 3/5 | Val Loss: 0.1320 | Val Acc: 0.9601
Epoch: 4/5 | Val Loss: 0.1161 | Val Acc: 0.9654
Epoch: 5/5 | Val Loss: 0.1173 | Val Acc: 0.9666

There is some variability in the folds, but that is not too bad for our first attempt.