Autoencoders

A simple autoencoder like the one we will study in this section is not commonly used for generative models, but the knowledge of autoencoders is fundamental to studying more powerful architectures called variational autoencoders.

We use some variable \mathbf{X} undefined as an input into an autoencoder. This could be a vector input in a fully connected neural network, but an autoencoder is also often used with images in combination with a convolutional neural network. An autoencoder is trained in an unsupervised way, without using any additional labels. Specifically the input and the output of an autoencoder are identical. So if we use an image as an input, we expect the output of the neural network, \mathbf{X}' undefined , to be as close as possible to the original input image.

An autoencoder consists of two components: an encoder and a decoder.

The encoder takes the input image \mathbf{X} undefined and produces the latent variable vector \mathbf{z} undefined . With each layer we keep decreasing the dimensionality of hidden values until we arrive at the so called bottleneck: the last layer of the encoder that outputs a relatively low dimensional vector. By decreasing the dimensionality we compress the information that is contained in the input, until we reach the highest compression point with at the bottleneck.

The decoder does the exact opposite. It takes the latent variable vector \mathbf{z} undefined as an input and tries to uncompress the information into the original space. With each layer the dimnesionality of the vector increases, until the neural network reaches the original dimensionality.

The neural network has to learn to produce \mathbf{\hat{X}} undefined , that is as close as possible to the input. As we squeeze a high dimensional image into a low dimensional vector, the compression is lossy and the output image might lose some detail, but if the network is expressive enough, the loss won't be dramatic.

Intuitively we could argue, that the neural network removes all the unnecessary noise, until only the relevant characteristics of the data that are contained in the latent space are left.

In our implementation below we create two nn.Sequential modules: one for the encoder and the other for the decoder. The encoder uses a stack of convolutional layers and a single fully connected layer to compress MNIST images into a 10 dimensional vector. The decoder uses transposed convolutions to decompress the image into a 1x28x28 dimensional tensor. The last layer of the decoder is a sigmoid activation function, because we scale the original images between 0 and 1.

class Autoencoder(nn.Module):
    def __init__(self):
        super().__init__()

        self.encoder = nn.Sequential(
            nn.Conv2d(in_channels=1, out_channels=16, kernel_size=3),
            nn.ReLU(inplace=True),
            nn.Conv2d(in_channels=16, out_channels=32, kernel_size=3),
            nn.ReLU(inplace=True),
            nn.Conv2d(in_channels=32, out_channels=64, kernel_size=3, stride=2),
            nn.ReLU(inplace=True),
            nn.Conv2d(in_channels=64, out_channels=64, kernel_size=3, stride=2),
            nn.ReLU(inplace=True),
            nn.Flatten(),
            nn.Linear(in_features=1600, out_features=10),
        )

        self.decoder = nn.Sequential(
            nn.Linear(in_features=10, out_features=1600),
            nn.ReLU(inplace=True),
            nn.Unflatten(1, (64, 5, 5)),
            nn.ConvTranspose2d(
                in_channels=64, out_channels=64, kernel_size=3, stride=2
            ),
            nn.ReLU(inplace=True),
            nn.ConvTranspose2d(
                in_channels=64,
                out_channels=32,
                kernel_size=3,
                stride=2,
                output_padding=1,
            ),
            nn.ReLU(inplace=True),
            nn.ConvTranspose2d(in_channels=32, out_channels=16, kernel_size=3),
            nn.ReLU(inplace=True),
            nn.ConvTranspose2d(in_channels=16, out_channels=1, kernel_size=3),
            nn.Sigmoid(),
        )

    def forward(self, x):
        x = self.encoder(x)
        x = self.decoder(x)
        return x

We use the mean squared error to minimize the distance between the original and reconstructed images and end up with the following results after 20 epochs of training.

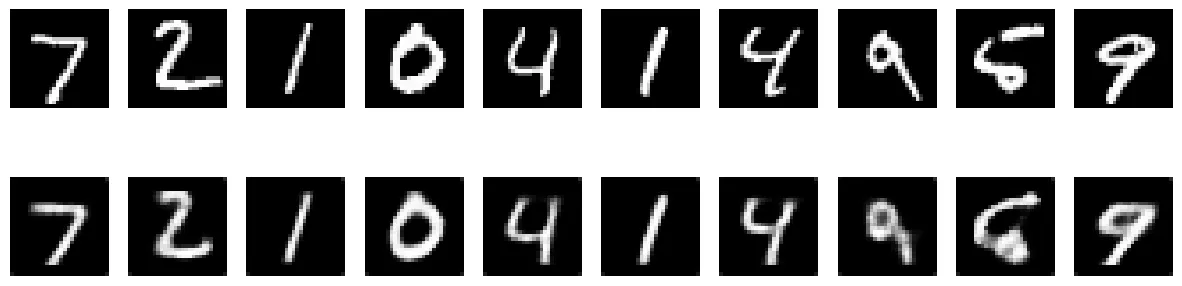
The top row depicts 10 original images from the validation dataset and the bottom row shows the recconstructed images that went through a 10 dimensional bottleneck. While the reconstruction made the images blurry, the quality is outstanding, especially given that we compressed those images from a 28x28 dimensional vector into a 10 dimensional vector.

While compressing the images into a lower dimensional space is an important task, we would like to use an autoencoder to generate new images and we can theoretically utilize the decoder for that purpose. Think about it, the decoder takes the latent variable vector and produces an image from a low dimensional space. The problem with this vanilla autoencoder is that we have no built-in mechanism to sample new latent variables from which we could generate the images. A variational autoencoder on the other hand is specifically designed for the purpose to generate new samples. We will study and utilze this architecture in the next section.