Skip Connections

If we had to pick just one invention in deep learning, that had allowed us to train truely deep nearal networks, it would most likely be skip connections. This technique is the bread and butter of many modern-day AI researchers and practicioners. If you removed skip connections from state of the art deep learning architectures, most of them would fall apart. So let's have a look at them.

Usually we expect deep neural networks to perform better than their shallow counterparts. Deeper architecures have more parameters and should be able to model more complex relationships. Yet when we increase the number of layers, training becomes impractical and performance deteriorates. While the usual suspect is the vanishing gradient problem, He et al.[1] were primarily motivated by the so called degradation problem, when they developed the ResNet (residual network) architecure. In this section we are going to cover both possibilities: we will discuss how skip connections might reduce the risk of vanishing gradients and we will discuss the degradation problem. As with many other techniques in deep learning, we know that a certain architecture works empirically, but often we do not know exactly why.

In the arcitectures that we covered so far, data flows from one calculation block into the next, from net inputs to activations and vice versa.

When we add skip connections, we add an additional path for the data to flow. Additionally to flowing into the next net input layer directly, the output of an activation is routed directly into one of the future activation layers. The streams from the net input and a previous activation are joined through a simple summation and the sum is used as input into the following activation function.

Usually when we calculate the output of a neuron, we just pass the net input through the activation function f undefined .

With skip connections what we actually calculate are the so called residual values.

The residuals are basically the differences between the actual net inputs and the outputs from the previous layer.

Theoretically skip connections should produce the same results, because we are not changing our task completely, we are just reformulating it. Yet the reality is different, because training deep neaural networks with skip connections is easier.

Let's imagine we face the usual problem of vanishing gradients. In a certain layer the information flow stops, because the gradient gets close to zero. Once that happens, all the preceding layers don't get their gradients updated due to the chain rule and training essentially stops.

If we have skip connections on the other hand, information can flow through the additional connection. That way we can circumvent the dead nodes in the neural network and the gradients can keep flowing.

The authors of the ResNet paper argued, that the vanishing gradient problem has been solved by modern activation functions, weight inintialization schemes and batch normalization. The degradation problem therefore had to have a different origin.

Let's discuss the example below to try to understand the problem. If we start with the yellow network and add an additional (blue) layer, we would expect the performance to be at least as good as that of the smaller (yellow) one.

If the yellow network has already achieved the best performance, the addional layer should learn the identity function.

That statement should apply, no matter how many additional layer we add. Performance should not deteriorate, because the last layers can always learn to output the input of the previous layer without change. Yet we know that shallow neural networks often outperform their deep counterparts.

Maybe it is not as easy to learn the identity function as we imagine. The neural network has to find the weights that exactly reproduce the input and this is not always a trivial task.

Skip connections on the other hand make it easy for the neural network to create an idenity functoin. All the network has to do is to set the weights and biases to 0.

If we use the ReLU activation function, the equality above will hold, because two ReLUs in a row do not change the outcome.

Impelementing skip connectins in PyTorch is a piece of cake. Below we create a new module called ResBlock. The block implements a skip connection by adding the input of the module to the output of the activation function.

class ResBlock(nn.Module):
    def __init__(self):
        super().__init__()
        self.linear = nn.Linear(HIDDEN, HIDDEN)
        
    def forward(self, features):
        output = F.relu(self.linear(features))
        return features + output

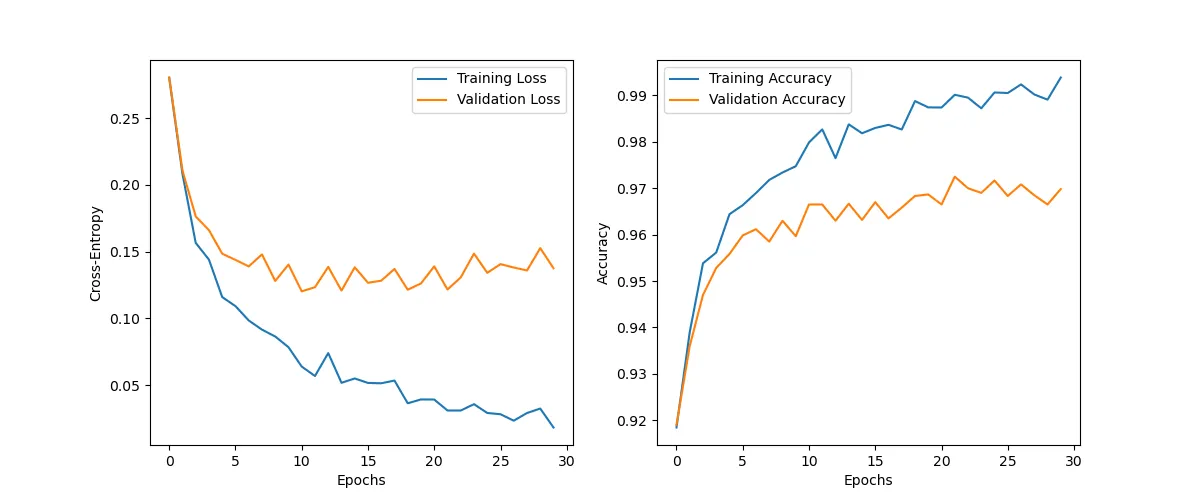
We implement our model by stacking 20 of residual blocks and we train the model on the MNIST dataset.

class Model(nn.Module):
    def __init__(self):
        super().__init__()
        self.layers = nn.Sequential(
                nn.Flatten(),
                nn.Linear(NUM_FEATURES, HIDDEN),
                nn.ReLU(),
                ResBlock(),
                ResBlock(),
                ResBlock(),
                ResBlock(),
                ResBlock(),
                ResBlock(),
                ResBlock(),
                ResBlock(),
                ResBlock(),
                ResBlock(),
                ResBlock(),
                ResBlock(),
                ResBlock(),
                ResBlock(),
                ResBlock(),
                ResBlock(),
                ResBlock(),
                ResBlock(),
                ResBlock(),
                ResBlock(),
                nn.Linear(HIDDEN, NUM_LABELS),
            )
    
    def forward(self, features):
        return self.layers(features)

While we can observe some overfitting, we do not have any trouble training such a deep neaural network.