Weight Initialization

Previously we had mentioned that weights can contribute to vanishing and exploding gradients. For the most part we adjust weights in a completely automated process by using backpropagation and applying gradient descent. For that reason we do not have a lot of influence on how the weights develop. The one place where we directly determine the distribution of weights is during the initialization process. This section is going to be dedicated to weight initialization: the pitfalls and best practices.

The first idea we might come up with is to initialize all weights equally, specifically to use 0 as the starting value for all weights and biases.

We will use this simple neural network to demonstrate the danger of such initialization. All we need to do is to work through a single forward and backward pass to realize the problem.

We will make the simplifying assumption, that there are no activation functions in the neural network and that we want to minimize the value of the output neuron and not some loss function. These assumptions do not have any effect on the results, but simplify notation and the depiction of the computational graph.

If we have the same weight w undefined for all nodes and layers, then in the very first forward pass all the neurons from the same layer will produce the same value.

When we apply backpropagation we will quickly notice that the gradients with respect to the weights of the same feature are identical in each node.

The same starting values and the same gradients can only mean that all nodes in a layer will always have the same value. This is no different than having a neural network with a single neuron per layer. The network will never be able to solve complex problems. And if you initialize all your weights with zero, the network will always have dead neurons, always staying at the 0 value.

Now let's use the same neural network and actually work though a dummy example. We assume feature values of 5 and 2 respectively and initialize all weights to 1.

Essentially you can observe two paths (left path and right path) in the computational graph above, representing the two neurons. But the paths are identical in their values and in their gradients. Even though there are 6 weights in the neural network, half of them are basically clones.

In order to break the symmetry researchers used to apply either a normal distribution (e.g. \mu = 0 undefined and \sigma = 0.1 undefined ) or a uniform distribution (e.g in the range -0.5 \text{ to } 0.5 undefined ) to initialize weights. This might seem reasonable, but Glorot and Bengio[1] showed that it is much more preferable to initialize weights based on the number of neurons that are used as input into the layer and the number of neurons that are inside a layer. This initializiation technique makes sure, that during the forward pass the variance of neurons stays similar from layer to layer and during the backward pass the gradients keep a constant variance from layer to layer. That condition reduces the likelihood of vanishing or exploding gradients. The authors proposed to initialize weights either using a uniform distribution \mathcal{U}(-a, a) undefined where a = \sqrt{\dfrac{6}{fan_{in} + fan_{out}}} undefined or the normal distribution \mathcal{N}(0, \sigma^2) undefined , where \sigma = \sqrt{\dfrac{2}{fan_{in} + fan_{out}}} undefined .

The words fan_{in} undefined and fan_{out} undefined stand for the number of neurons that go into the layer as input and the number of neurons that are in the layer respectively. In the below example in the first hidden layer fan_{in} undefined would be 2 and fan_{out} undefined would be 3 respectively. In the second hidden layer the numbers would be exactly the other way around.

While the Xavier/Glorot initialization was studied in conjunction with the sigmoind and the tanh activation function, the Kaiming/He initialization was designed to work with the ReLU activation[2] . This is the standard initialization mode used in PyTorch.

Implementing weight initialization in PyTorch is a piece of cake. PyTorch provides in nn.init different functions that can be used to initialize a tensor. You should have a look at the official PyTorch documentation if you would like to explore more initialization schemes. Below for example we use the Kaiming uniform initialization on an empty tensor. Notice that the initialization is done inplace.

W = torch.empty(5, 5)
# initializations are defined in nn.init
nn.init.kaiming_uniform_(W)

tensor([[-0.9263, -0.0416,  0.0063, -0.8040,  0.8433],
        [ 0.3724, -0.9250, -0.2109, -0.1961,  0.3596],
        [ 0.6127,  0.2282,  0.1292,  0.8036,  0.8993],
        [-0.3890,  0.8515,  0.2224,  0.6172,  0.0440],
        [ 1.0282, -0.7566, -0.0305, -0.4382, -0.0368]])

When we use the nn.Linear module, PyTorch automatically initializes weights and biases using the Kaiming He uniform initialization scheme. The sigmoid model from the last section was suffering from vanishing gradients, but we might remedy the problem, by changing the weight initialization. The Kaiming|He initialization was developed for the ReLU activation function, while the Glorot|Xavier initialization should be used with sigmoid activation functions. We once again create the same model that uses sigmoid activation functions. Only this time we loop over weights and biases and use the Xavier uniform initialization for weights and we set all biases to 0 at initialization.

class SigmoidModel(nn.Module):
    def __init__(self):
        super().__init__()
        self.layers = nn.Sequential(
            nn.Flatten(),
            nn.Linear(NUM_FEATURES, HIDDEN),
            nn.Sigmoid(),
            nn.Linear(HIDDEN, HIDDEN),
            nn.Sigmoid(),
            nn.Linear(HIDDEN, HIDDEN),
            nn.Sigmoid(),
            nn.Linear(HIDDEN, HIDDEN),
            nn.Sigmoid(),
            nn.Linear(HIDDEN, HIDDEN),
            nn.Sigmoid(),
            nn.Linear(HIDDEN, NUM_LABELS)
        )
        
        self.reset_parameters()
        
    def reset_parameters(self):
        with torch.inference_mode():
            for param in self.parameters():
                if param.ndim > 1:
                    nn.init.xavier_uniform_(param)
                else:
                    param.zero_()
            
    def forward(self, features):
        return self.layers(features)

model = SigmoidModel().to(DEVICE)
criterion = nn.CrossEntropyLoss(reduction="sum")
optimizer = optim.SGD(model.parameters(), lr=ALPHA)

This time around the model performs much better.

history = train(train_dataloader, val_dataloader, model, criterion, optimizer)

Epoch: 1/30 | Train Loss: 2.308537656906164 | Val Loss: 2.308519915898641
Epoch: 10/30 | Train Loss: 0.20434634447115443 | Val Loss: 0.2530187802116076
Epoch: 20/30 | Train Loss: 0.07002673296947375 | Val Loss: 0.15957480862239998
Epoch: 30/30 | Train Loss: 0.04259131510365781 | Val Loss: 0.1637446080291023

plot_history(history, "xavier_metrics")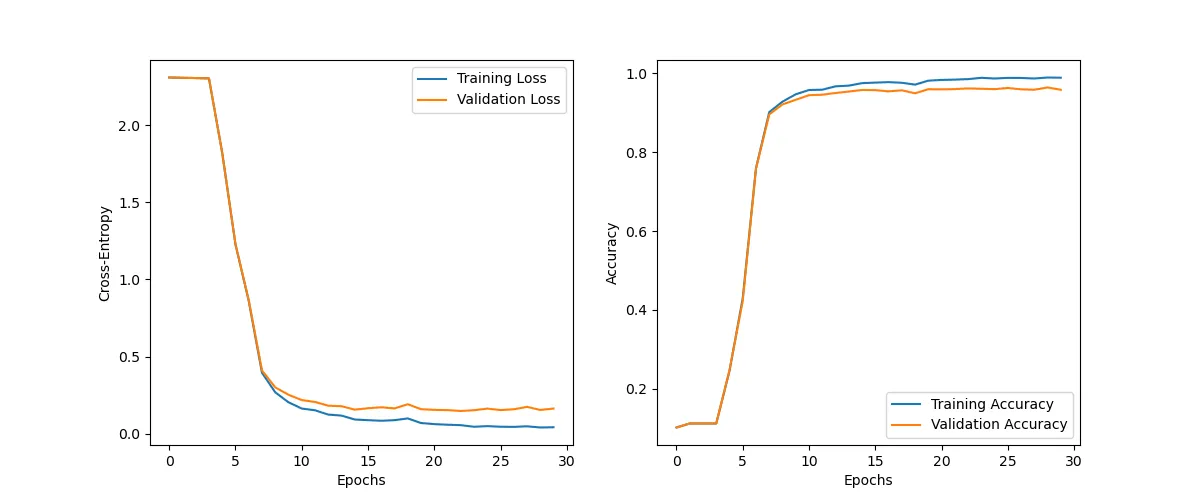

You should still use the ReLU activation function for deep neural networks, but be aware that weight initialization might have a significant impact on the performance of your model.